Option Adjusted Spread

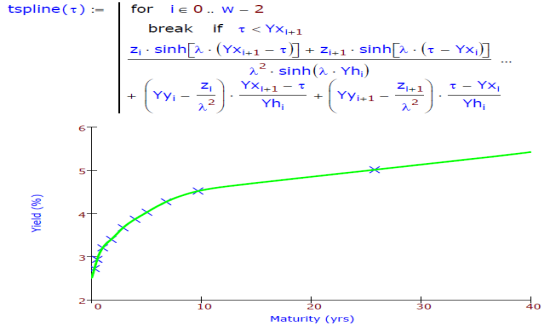
Spread Adjustment Yields

Often bonds are issued with embedded options. This makes the standard algorithms for computing yield from the given price or price from an yield, quite irrelevant.

We have explained here some of the details of the option-adjusted spread (OAS) model for a callable bond using the BMA OAS formula.

The model uses spline in tension algorithm to derive the bond yields at a specified tenor τ, based on the yields of reference government bonds (marked by an x in the graph). These yields are then used to compute the present value of the target bond that has an embedded option.

Baseline Spot Rate

The model uses the following attributes of the target bond to compute the cash-flows.

• sd: Settlement date.
• pcd: Previous coupon date or issue date.
• ced: Call exercise date
• lcd: Last coupon date
• md: Maturity date

The baseline discount factor and one-period forward-forward rate functions use the spread adjusted yields calculated above. These functions are used later by the model.

• The discount factors are used to compute the present value of the cash-flows.
• The OAS δ is the constant spread on top of the one-period forward-forward rate.

OAS Adjusted Rate

The model then defines functions for the OAS δ adjusted forward-forward rates and the discount factors. The present values of cash-flows based on these discount factors should then match the current market price of the bond.

The skew adjustment formula also uses the historical volatility to compute the value of the embedded option. Due to market movements over time, it is possible that the current forward-forward rates are quite different from the bond coupon rates. To take care of this gap, the model adjusts the historical volatility, which is later used to get the value of the embedded option.

ECS Pricing Formula

The P_bullet(δ) function gives the current value of the target bond cash-flows for the given OAS δ.

The P_option(δ) function gives the value of the embedded optionality for the given OAS δ. For pricing the optionality, we use a modified Black-Scholes model. Note that vs(δ) is the spread adjusted volatility discussed above.

Calculated dirty price of the bond P_full(δ) is the bond price P_bullet(δ) minus the value of the option P_option(δ). Note that as we are using the actual coupon dates, the prices computed by these formulae include the accrued interest and therefore no further adjustment is required for the dirty price.

OAS Value From Purchase Price

The model finally defines a function Oas(P_purchase) that uses Newton-Raphson method to estimate the OAS δ.

The OAS is therefore the constant spread over the forward-forward bond yield curve that makes the price of the bond equal to its market price P_purchase. This OAS value considers the embedded option in the target bond.

We had implemented the BMA OAS model when it was still being developed. Apart from simply implementing the model, we contributed to its development by communicating certain issues and their resolution to BMA.