Credit Default Swap

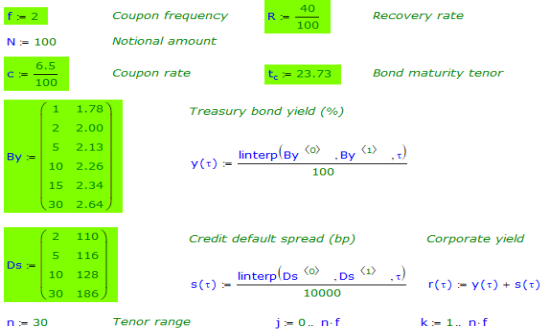
Government and Corporate Bond Yield Curves

Before discussing the actual algorithm, let us first understand the nomenclature from the description of CDS in the previous page.

• The company is the reference entity.
• The default by the company is known as the credit event.
• The bond is known as the reference obligation.
• The total value of the bond that can be sold is the notional principal.

There are few models available in the public domain, which can be used to price a CDS. We have explained one of them here, which uses the recovery rate, the yields of government and corporate bonds to price the CDS.

In some markets, corporate bonds (of the reference entity) are traded as a spread (in basis-points) over the government bond yields.

Discount Factor Curves

The model first computes the discount factors for both the government and corporate bonds at a fixed compounding frequency (half-yearly in our case).

For computing the discount factors, we find the zero-coupon rates for each tenor at the given compounding frequency. This is done in an incremental manner. For example, to find the zero-coupon rate at tenor k, the model uses the zero-coupon rates for tenors 1 to k-1.

The discount factors at each compounding frequency are then directly derived from the zero-coupon rates.

Corporate Bond Values

The present value of the reference bond is computed by discounting all the future cash-flows (coupons and the principal) to spot by using the corporate discount factor curve.

The model then derives the forward value of the reference bond at each future tenor, assuming a credit event occurs.

The loss value function gives the difference between the future value and the recovery value, discounted to spot using the treasury discount curve.

CDS Present Value

Like any insurance policy, a CDS also requires payments of a premium amount at equal intervals (quarterly in our case) to maintain the contract.

Function SV(s, t) is the present value of the future premium amounts and the accrued coupon interest at the time of a given credit event.

Note that the strike rate s is the target value to be computed by the model. Therefore, this function will be later used iteratively by the model to find the strike rate for the CDS.

Default Probability Distribution

If P.δτ is the probability of default between time τ and τ+δτ, then P is the default probability density.

If we assume the default probability density between τ and τ+δτ to be a constant, we can compute the loss amount between two time periods using Simpson’s rule with δτ as a single day.

The probability of default is now computed based on the difference in interest rates offered by the corporate bonds over the government bonds.

Value of CDS

A strike rate s that makes the claim amount V(s) equal to zero, is the CDS par rate. The V(s) can either be inclusive of accrued interest or not, depending on the CDS contract.

Finally, we define a function to compute the value of a CDS, given the strike rate s. The CDS value is the difference between the cash outflow and inflow. The outflow is the money paid at the credit event, above the recovery value of the bond. The inflow is the premium paid during the tenure of the swap.